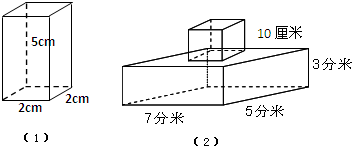
考点:长方体和正方体的表面积,长方体和正方体的体积,组合图形的体积
专题:立体图形的认识与计算
分析:(1)根据长方体的特征,12条棱分为互相平行的3组,每组4条棱的长度相等,6个面是长方形(特殊情况有两个相对的面是正方形),相对的面的面积相等.
长方体的棱长总和=(长+宽+高)×4,表面积s=(ab+ah+bh)×2,体积v=abh,把数据代入公式解答.
(2)正方体的表面积公式:s=6a2,体积公式:v=a3,先求出长方体的表面积,再加上正方体4个面的面积即得其表面积;其体积就等于长方体的体积加上正方体的体积.解答即可.
解答:
解:(1)棱长总和:
(2+2+5)×4
=9×4
=36(厘米)
表面积:
(2×5+2×5+2×2)×2
=(10+10+4)×2
=24×2
=48(平方厘米)
体积:
2×2×5=20(立方厘米)
答:它的棱长总和是36厘米,表面积是48平方厘米,体积是20立方厘米.
(2)10厘米=1分米
表面积:(7×5+5×3+7×3)×2+1×1×4
=142+4
=146(平方分米)
7×5×3+1×1×1
=105+1
=106(立方分米)
答:它的表面积是146平方分米、体积是106立方分米
故答案为:(1)36厘米,48平方厘米,20立方厘米;(2)146平方分米、106立方分米.
点评:此题主要考查正方体和长方体的特征、棱长总和、表面积和体积的计算,直接把数据代入公式进行解答.