
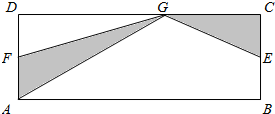
 如图,ABCD是一个长方形,AB=20m,AD=5m,E、F分别是BC、AD上的中点,G是线段DC上任意一点,你知道阴影部分面积是多少吗?
如图,ABCD是一个长方形,AB=20m,AD=5m,E、F分别是BC、AD上的中点,G是线段DC上任意一点,你知道阴影部分面积是多少吗? 分析 根据三角形的面积等于底乘高除以2,用含有字母的式子表示出三角形AFG的面积和三角形CEG的面积,再把这两个面积相加就是阴影部分的面积.
解答 解:阴影部分的面积就是△AFG的面积加△CEG的面积的和.
△AFG的面积=AF×DG×$\frac{1}{2}$
=$\frac{1}{2}$AD×DG×$\frac{1}{2}$
=$\frac{1}{4}$AD×DG,
△CEG的面积=CE×GC×$\frac{1}{2}$
=$\frac{1}{2}$AD×GC×$\frac{1}{2}$
=$\frac{1}{4}$AD×GC,
△AFG的面积+△CEG的面积=$\frac{1}{4}$AD×DG+$\frac{1}{4}$AD×GC
=$\frac{1}{4}$AD×(DG+GC)
=$\frac{1}{4}$×AD×DC
=$\frac{1}{4}$×AD×AB
=$\frac{1}{4}$×5×20
=25(平方米)
答:阴影部分面积是25平方米.
点评 两个阴影部分的三角形的底是长方形宽的一半,高相加是长方形的长,所以阴影部分的面积是长方形宽的一半乘长再除以2.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
 $\frac{15}{16}$
$\frac{15}{16}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com