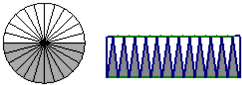
数学课上李老师将一个底面半径是5厘米,高10厘米的圆柱分解成若干个扇形体,再拼成一个近似的长方体,这个长方体的表面积是多少平方厘米?
解:拼成的长方体的长是5π厘米;宽是5厘米,高是原来圆柱的高10厘米,所以这个长方体的表面积是:
(5π×5+5π×10+5×10)×2,
=(25π+50π+50)×2,
=(75π+50)×2,
=150π+100,
=471+100,
=571(平方厘米);
答:这个长方体的表面积是571平方厘米.
分析:根据圆柱的切割方法与拼组特点可知:拼成的长方体的长是圆柱底面周长的一半,即是5π厘米;宽是半径的长度是5厘米,高是原来圆柱的高10厘米,由此利用长方体的表面积公式,代入数据即可解答.
点评:根据圆柱切割后拼组长方体的特点,得出这个长方体的长宽高是解决此类问题的关键.



