解:(1)2005-999,
=2005-(1000-1),
=2005-1000+1,
=1006;
(2)0.25+
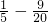
,
=0.25+0.2-0.45,
=0;
(3)
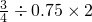
,
=0.72÷0.75×2,
=2;
(4)
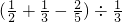
,
=(

+

-

)×3,
=

×3+

×3-

×3,
=

+1-

,
=0.3;
(5)
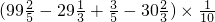
,
=[(99

+

)-(29

+30

)]×

,
=40×

,
=4;
(6)
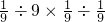
,
=

×

×

×9,
=
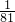
;
(7)11×991+99,
=11×991+11×9,
=11×(991+9),
=11000;
(8)
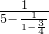
,
=
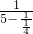
,
=

,
=1;
(9)1+3+5+7+9+11+13+15+17+19,
=(1+19)+(3+17)+(5+15)+(7+13)+(9+11),
=20×5,
=100;
(10)
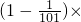
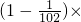
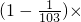
…×
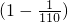
,
=
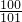
×
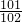
×
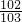
×…×
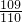
,
=
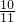
.
分析:(1)把999看作1000,然后加1;
(2)、(3)把分数都化为小数,进行计算;
(4)先根据除以一个分数,等于乘这个分数的倒数,然后运用乘法分配律进行解答;
(5)先把括号里的运算进行交换,再结合,进行简算,然后再和

相乘;
(6)按照乘除法计算方法进行解答;
(7)把99分解成11×9,然后运用乘法分配律进行简算;
(8)先算1-

=

,再算1÷

=4,继而算5-4=1,最后算1÷1=1;
(9)首位进行结合,再运用乘法分配律进行解答;
(10)分别算出括号里的,然后相乘,进行约分,即可.
点评:解答此题的关键:熟练掌握加、减、乘、除中的一些运用定律和性质,能根据数的特点,运用简便方法,进行简算.

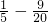 =
=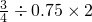 =
=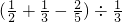 =
=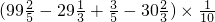 =
=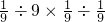 =
=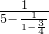 =
=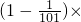
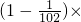
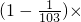 …×
…×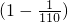 =
=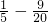 ,
,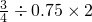 ,
,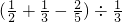 ,
, +
+ -
- )×3,
)×3, ×3+
×3+ ×3-
×3- ×3,
×3, +1-
+1- ,
,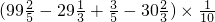 ,
, +
+ )-(29
)-(29 +30
+30 )]×
)]× ,
, ,
,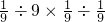 ,
, ×
× ×
× ×9,
×9,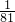 ;
;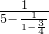 ,
,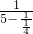 ,
, ,
,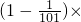
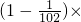
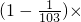 …×
…×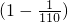 ,
,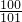 ×
×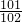 ×
×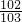 ×…×
×…×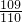 ,
,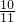 .
. 相乘;
相乘; =
= ,再算1÷
,再算1÷ =4,继而算5-4=1,最后算1÷1=1;
=4,继而算5-4=1,最后算1÷1=1;

 快乐5加2金卷系列答案
快乐5加2金卷系列答案