分析:我们可以先过图中的点横向作一条垂线,由于是正方形上面是一个半圆则下面也会是一个和上面一样的半圆,正方形就被分成了上下相等的两个长方形,我们可以分求出上的阴影部分的面积就是一个直径是正方形边长的半圆,我们可以设正方形的边长为a,则圆的半径就是
,则半圆的面积是:
π
()2即是
πa
2,而下面空白的两部分合起来刚好也是个半圆,则阴影部分的面积就是长方形的面积-下面半圆的面积:
a×a-
πa
2,则图中上下阴影部分的面积相加得:
a×a-
πa
2+
πa
2=
a×a,由于正方形的面积是a
2,故阴影部分和正方形的面积比是:
a
2:a
2=1:2,故答案是:1:2.
解答:解:我们可以先过图中点横向作一条垂线,因为图形是个正方形,上面是个半图则这过一点横向作的垂线可以分为上下相等的两个长方形的,
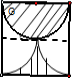
我们先设正方形的边长是a,宽就是
,则面积就是:
a
2,
由于下方形边长为a,则上面半圆的半径就是
,则上边阴影部分的面积是:
π
()2即是
πa
2;
则下面白的两个部分刚好是个半圆则面积是:a×
-
×π×
()2=
-
πa
2,
则图中阴影部分的面积共是:
a
2-
πa
2+
πa
2即是:
a
2,
则图中阴影部分和正方形的面积比是:
a
2:a
2=1:2.
故答案是1:2.
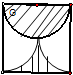
点评:本题考查我们利用作辅助线把正方形分成上下完全相等的两个长方形,然后利用圆的面积公式,分别求出上面的阴影部的面积和下面的阴影部分的面积后,再相加得出总的阴影部分的面积后,在和正方开的面积作比进行解决问题.




 阅读快车系列答案
阅读快车系列答案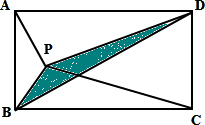 (2004?宜兴市)如图,ABCD是一个长方形.三角形PAB、PBC和PCD的面积分别是44平方厘米,144平方厘米和260平方厘米.图中阴影部分的面积是( )
(2004?宜兴市)如图,ABCD是一个长方形.三角形PAB、PBC和PCD的面积分别是44平方厘米,144平方厘米和260平方厘米.图中阴影部分的面积是( ) 用数对表示出图中扇形AOB三个点的位置.A(
用数对表示出图中扇形AOB三个点的位置.A(