Question

用小棒按照如图所示方式摆图形．
（1）摆n个八边形需要（　　）根小棒．
（2）2014根小棒可以摆

 

个八边形，还多

 

根小棒．

Answer 1

考点：数与形结合的规律

专题：探索数的规律

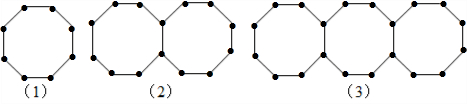
分析：摆一个八边形用了8根小棒，摆两个八边形就多用了7根，摆三个就多用了7×2根，…能够根据图形发现规律：多一个八边形，就多用7根小棒，则在第n个图形中，需要小棒：8+7（n-1）=7n+1根；把2014代入7n+1中，求出n的数量即可．

解答： 解：（1）在第n个图形中，需要小棒：
8+7（n-1）=7n+1（根）
答：摆n个八边形需要7n+1根小棒．

（2）7n+1=2014
7n=2014-1
7n=2013
n是287还余4
答：2014根小棒可以摆287个八边形，还多4根小棒．
故答案为：287，4．

点评：此题主要培养学生的观察能力和总结能力，这里要抓住题干中图形的个数和小棒的增加情况，推理得出变化规律是解决此类问题的关键．