练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    如图所示，∠1+∠2+∠3+∠4+∠5+∠6等于
    360
    360
    度．
    分析：如图，∠3=∠7，所以∠2+∠3=180°-∠A；同理，∠6=∠8，所以∠1+∠6=180°-∠C；∠4+∠5=180°-∠B；
    由此把这三个式子加起来即可得出，∠1+∠2+∠3+∠4+∠5+∠6=180°×3-（∠A+∠B+∠C），又因为∠A+∠B+∠C=180°，所以，∠1+∠2+∠3+∠4+∠5+∠6=360°．
    解答：解：∠3=∠7，所以∠2+∠3=180°-∠A；
    同理，∠6=∠8，所以∠1+∠6=180°-∠C；
    ∠4+∠5=180°-∠B；
    则∠1+∠2+∠3+∠4+∠5+∠6，
    =180°×3-（∠A+∠B+∠C），
    =540°-180°，
    =360°，
    答：∠1+∠2+∠3+∠4+∠5+∠6=360°．
    故答案为：360．
    点评：此题考查三角形内角和定理的灵活应用，把这几个角转化到三角形ABC中，利用三角形的内角和定理即可解决问题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

    能否用500个如图所示的1×2的小长方形形成一个5×200的大长方形，使得5×200的长方形的每一行、每一列都有偶数个星？请说明理由．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    某市市区几个旅游景点的平面示意图如图所示，（2，2）表示明珠广场的位置．

    （1）写出湖心岛、光岳楼、展览中心的位置．
    （2）一位旅客游览的路线是（12，0）→（9，0）→（10，4）→（13，5），这位旅客依次去过哪些景点？

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    精英家教网如图所示：∠1=35°
    ∠2=
     

    ∠3=
     
    ．
    ∠4=
     
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

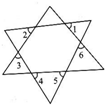    如图所示，∠1+∠2+∠3+∠4+∠5+∠6等于________度．

    查看答案和解析>>

    同步练习册答案