Question

19．如图所示，四边形ABCD为长方形，△AOE=5，△ABO=15，求阴影部分的面积．

Answer 1

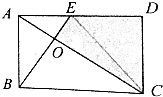
分析 因为S△_BEC=$\frac{1}{2}$S_{四边形ABCD}，S△_ABC=$\frac{1}{2}$S_{四边形ABCD}，所以S△_BEC=S△_ABC，所以S△_EOC=S△_AOB=15；
由“△_AOE的面积为5，△_ABO的面积为15”可得S_△AOE：S_△ABO=5：15=1：3，所以EO：OB=1：3，由此推出S_△OEC：S_△BOC=1：3，进而推得三角形BOC的面积，也就求出来长方形的面积，再根据求出的S_△EOC，和已知△AOE=5，求得阴影部分的面积，解决问题．

解答 解：因为S△_BEC=$\frac{1}{2}$S_{四边形ABCD}，
S△_ABC=$\frac{1}{2}$S_{四边形ABCD}，
所以S△_BEC=S△_ABC，
所以S△_EOC=S△_AOB=15，
因为△_AOE的面积为5，△_ABO的面积为15，
可得S_△AOE：S_△ABO=5：15=1：3，
所以EO：OB=1：3，
所以S_△OEC：S_△BOC=1：3，
所以S_△BOC=15×3=45，
所以长方形的面积为：
（S△_AOB+S△_BOC）×2
=（15+45）×2
=60×2
=120；
又因为S△_ADC=$\frac{1}{2}$S_{四边形ABCD}，
所以S△_ADC=120×$\frac{1}{2}$=60，
S△_EDC=60-S△_AOE-S△_OEC
=60-5-15
=40
所以阴影部分的面积：
S△_OEC+S△_EDC=15+40=55．
答：阴影部分的面积为55．

点评 此题关系较复杂，关键在于运用三角形之间便于面积的正比关系推出有关三角形的面积，解决问题．