
分析 此题关键是起点再起点相遇,实际上是求15与21的最小公倍数,根据求两个数的最小公倍数的方法:即15和21这两个数的公有质因数与独有质因数的连乘积;进行解答即可.
解答 解:因为:15=3×5,
21=7×3,
所以15和21的最小公倍数是:3×5×7=105;
答:至少105分钟后他们又在起跑点相遇.
点评 解此类题一定要认真读题,关键题意明白跑圈再次相遇 实际上是求他们跑一圈所用时间的最小公倍数.
本题还可以按追及相遇问题解答,第一次相遇的时间是:1÷($\frac{1}{15}-\frac{1}{21}$)=$\frac{105}{2}$(分钟),这时甲乙相遇的时间不是15和21的倍数,即相遇的地点不在出发点,所以应再行一个$\frac{105}{2}$分钟即可在出发点相遇,$\frac{105}{2}$×2=105(分钟).


科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 如图是一块长方形铁皮按1:60的比例画在图纸上的.这块铁皮正好可以做一个圆柱形水桶.
如图是一块长方形铁皮按1:60的比例画在图纸上的.这块铁皮正好可以做一个圆柱形水桶.查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
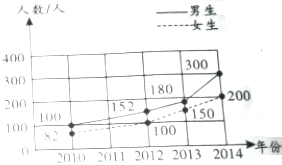 如图是某小学2010-2014年招生人数情况统计图
如图是某小学2010-2014年招生人数情况统计图查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com