练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    8．钝角三角形中最小的一个角一定小于45度．√．（判断对错）

    分析 钝角三角形中最大角的度数大于90°，由三角形的内角和是180°可以得到：另外两个内角的和应小于90°，因此这两个内角一定有一个角小于45°，从而问题得解．

    解答 解：因为钝角三角形中最大角的度数大于90°，
    则另外两个内角的和应小于90°，
    依据数量间的和差关系得：
    这两个内角一定有一个角小于90°÷2=45°．
    故答案为：√．

    点评 解答此题的关键是：利用已知条件及三角形的内角和定理得出另外两个内角的和应小于90°，再据数量间的和差关系得到这两个内角一定有一个角小于45°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：计算题

    18．直接写出得数
    452+98=1.25×8=640÷16=$\frac{1}{5}$×$\frac{1}{2}$÷$\frac{1}{5}$×$\frac{1}{2}$=45÷1.25÷8=
    5.01-1.8=0.25×0.4=0.88+0.12=6.5+9.5+3.5=（$\frac{3}{8}$-0.375）×5=

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    19．修路队修一段公路，第一天修了这段公路的30%，第二天比第一天多修20米，两天共修了440米，这段公路有多少米？

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    16．一件工作，甲单独完成需要10天，乙的工作效率是甲的$\frac{2}{3}$．甲乙合作几天可以完成任务？

    查看答案和解析>>

    科目：小学数学 来源： 题型：判断题

    3．两个数分别除以这两数的最大公约数，所得的商是互质数．√．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：操作题

    13．下面的折线统计图表示的是李明骑自行车从9时到11时由甲地到乙地行驶的路程．

    ①李明从甲地到乙地一共用了2小时．
    ②甲乙两地的路程是30千米．
    ③李明平均每小时行驶15千米．
    ④李明在途中停留的时间是0.5小时．
    ⑤李明在骑车行驶的最后30分钟行了15千米．

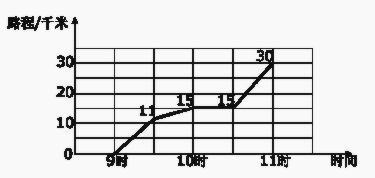
    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    20．在横线里填上“＞”“＜”或“=”
    3.45×0.01＜3.45÷$\frac{1}{100}$；
    0.25＞-2.5；
    $\frac{7}{8}$＜$\frac{11}{12}$．

    查看答案和解析>>

    科目：小学数学 来源： 题型：判断题

    17．分数单位大的分数一定大于分数单位小的分数．×．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    18．估算632÷90时，把632估成630除得的商最准确．

    查看答案和解析>>

    同步练习册答案