
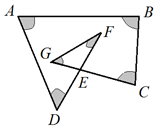
 如图中,∠A+∠B+∠C+∠D+∠F+∠G 等于360度.
如图中,∠A+∠B+∠C+∠D+∠F+∠G 等于360度. 分析 连接CD,有∠G+∠F=∠EDC+∠ECD,这样就转化成四边形的内角和了,四边形的内角和是360度.
解答 解:连接CD,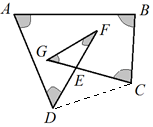
则∠G+∠F+∠FEG=∠EDC+∠ECD+∠FEG=∠=180°,
因为∠FEG=∠FEG
所以∠G+∠F=∠EDC+∠ECD,
所以∠A+∠B+∠C+∠D+∠F+∠G=∠A+∠B+∠BCE+∠EDC+∠ECD+∠ADE=(4-2)×180°=360°.
故∠A+∠B+∠C+∠D+∠F+∠G的度数是360°.
故答案为:360.
点评 考查了多边形内角与外角,三角形内角和定理,根据三角形的内角和定理把求角的和的问题转化为求多边形的内角和的问题.


科目:小学数学 来源: 题型:应用题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com