
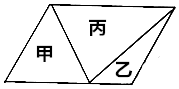
分析 根据图示,以及三角形面积公式可得:丙的面积=甲的面积+乙的面积,设平行四边形的面积是x,那么乙的面积就是$\frac{1}{5}$x,丙的面积=四边形面积-甲的面积-乙的面积,也就是x-48-$\frac{1}{5}$x=$\frac{4}{5}$x-48,再根据丙的面积=甲的面积+乙的面积,可列方程:48+$\frac{1}{5}$x=$\frac{4}{5}$x-48,依据等式的性质,求出x的值,再代入丙的面积即可解答.
解答 解:设平行四边形的面积是x,
丙的面积:x-48-$\frac{1}{5}$x=$\frac{4}{5}$x-48,
则 48+$\frac{1}{5}$x=$\frac{4}{5}$x-48
48+$\frac{1}{5}$x-$\frac{1}{5}$x=$\frac{4}{5}$x-48-$\frac{1}{5}$x
48+48=$\frac{3}{5}$x-48+48,
$\frac{3}{5}$x=96
$\frac{3}{5}$x÷$\frac{3}{5}$=96÷$\frac{3}{5}$
x=160
$\frac{4}{5}$×160-48
=128-48
=80(平方厘米)
答:丙的面积是80平方厘米,
故答案为:80.
点评 解答本题的关键是:明确丙的面积=甲的面积+乙的面积,用x分别表示出乙和丙的面积.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:小学数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com