

分析 连接OC,求阴影部分的面积,用$\frac{1}{3}$圆的面积减去减去三角形AOC的面积即可得到阴影部分的面积.
解答 解: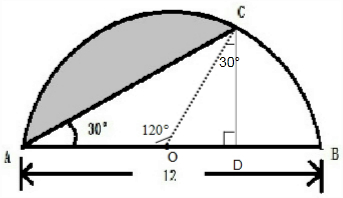
因为AB=12,OC=12÷2=6
在三角形OCD中,∠OCD=30°
所以OD=$\frac{1}{2}$OC=$\frac{1}{2}$×6=3,
所以CD2+OD2=OC2
CD2=36-9
即CD=3$\sqrt{3}$
所以三角形AOC的面积=6×3$\sqrt{3}$÷2=9$\sqrt{3}$.
阴影部分的面积:
3.14×(12÷2)2×$\frac{1}{3}$-9$\sqrt{3}$
=3.14×36×$\frac{1}{3}$-9$\sqrt{3}$
=37.68-9$\sqrt{3}$
答:阴影部分的面积37.68-9$\sqrt{3}$.
点评 本题运用圆的面积及三角形的面积公式进行解答即可.


 阅读快车系列答案
阅读快车系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
| 287+399= | 16×0.25= | 6÷40%= | $\frac{5}{12}$÷$\frac{1}{6}$= |
| 3.14×202= | 48×($\frac{1}{6}$-$\frac{1}{8}$)= | 1-1÷5-$\frac{1}{5}$= | $\frac{1}{49}$:$\frac{1}{7}$=$\frac{1}{7}$. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com