
 如图,5个等腰直角三角形叠放在一起,它们的斜边都在一条直线上,已知最小的等腰直角三角形的斜边长是4厘米,其余等腰三角形的斜边依次多4厘米,则图中阴影部分的面积________是平方厘米.
如图,5个等腰直角三角形叠放在一起,它们的斜边都在一条直线上,已知最小的等腰直角三角形的斜边长是4厘米,其余等腰三角形的斜边依次多4厘米,则图中阴影部分的面积________是平方厘米.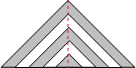


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:小学数学 来源: 题型:
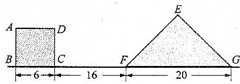 如图所示正方形ABCD与1个等腰直角三角形EFG(EF=EG),放在同一直线上.现在三角形不动,正方形以每秒2厘米的速度向右沿直线匀速运动.试回答以下情况时,正方形与三角形重叠部分的面积是多少?
如图所示正方形ABCD与1个等腰直角三角形EFG(EF=EG),放在同一直线上.现在三角形不动,正方形以每秒2厘米的速度向右沿直线匀速运动.试回答以下情况时,正方形与三角形重叠部分的面积是多少?查看答案和解析>>
科目:小学数学 来源: 题型:
 把一张长25厘米,宽20厘米的长方形纸裁成直角边都是5厘米的等腰直角三角形(如图,每个方格代表边长1厘米).至少裁成多少个?(先在图里画一画,再解答)
把一张长25厘米,宽20厘米的长方形纸裁成直角边都是5厘米的等腰直角三角形(如图,每个方格代表边长1厘米).至少裁成多少个?(先在图里画一画,再解答)查看答案和解析>>
科目:小学数学 来源: 题型:
 如图,5个等腰直角三角形叠放在一起,它们的斜边都在一条直线上,已知最小的等腰直角三角形的斜边长是4厘米,其余等腰三角形的斜边依次多4厘米,则图中阴影部分的面积
如图,5个等腰直角三角形叠放在一起,它们的斜边都在一条直线上,已知最小的等腰直角三角形的斜边长是4厘米,其余等腰三角形的斜边依次多4厘米,则图中阴影部分的面积查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com