
 如图,每个图案都是由若干个棋子摆成,依照此规律,第100个图案中棋子的总个数是10100.
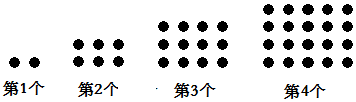
如图,每个图案都是由若干个棋子摆成,依照此规律,第100个图案中棋子的总个数是10100. 分析 观图可知,第1个图案的纵队棋子个数是:1,横队棋子个数2即1+1,总个数=1×(1+1)=2个;第2个图案的纵队棋子个数是:2,横队棋子个数3即2+1,总个数=2×(2+1)=6个;第3个图案的纵队棋子个数是:3,横队棋子个数4即3+1,总个数=3×(3+1)=12个…所以当第n个图案的纵队棋子个数是:n,横队棋子个数是:n+1,那么第n个图案中棋子的总个数与n的关系式为:总个数=n(n+1).当n=100时,代入解答即可.
解答 解:由分析可得:
每个图案的纵队棋子个数是:n,
每个图案的横队棋子个数是:n+1,
那么第n个图案中棋子的总个数与n的关系式为:总个数=n(n+1).
那么第100个图案中棋子的总个数:
100×(100+1)
=100×101
=10100(个)
答:第100个图案中棋子的总个数是10100个.
故答案为:10100.
点评 本题主要考查图形的变化规律:首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善于联想来解决这类问题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com