Question

探索：
如图，外层正方形边长是5，往里第二、三、四、五层各小正方形边长依次是4、3、2、1，观察图形，完成下列问题；
（1）判断大小关系：1³+2³+3³+4³+5³________（1+2+3+4+5）²；
（2）结合图形，证明你（1）中的判断．
猜想：
1³+2³+3³+…+n³=________．

Answer 1

解：（1）1³+2³+3³+4³+5³=1+8+27+64+125=225；
（1+2+3+4+5）²=15²=225；
所以1³+2³+3³+4³+5³=（1+2+3+4+5）²．
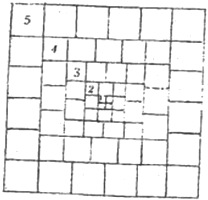
（2）结合图形：大正方形的面积等于所有小正方形的面积之和为：
5²×20+4²×16+3²×12+2²×8+1²×4，
=5²×5×4+4²×4×4+3²×3×4+2²×2×4+1²×1×4，
=5³×4+4³×4+3³×4+2³×4+1³×4，
=（5³+4³+3³+2³+1³）×4；
同时，大正方形的边长为：（1+2+3+4+5）×2，
所以面积为：
[1+2+3+4+5）×2]×[1+2+3+4+5）×2]，
=[（1+2+3+4+5）×2]²
=（1+2+3+4+5）²×2²，
=（1+2+3+4+5）²×4；
所以：（5³+4³+3³+2³+1³）×4=（1+2+3+4+5）²×4；
即：1³+2³+3³+4³+5³=（1+2+3+4+5）²．
（3）由以上结论猜想得出：
1³+2³+3³+…+n³=（1+2+3+…+n）²．
故答案为：（1）=；猜想：（1+2+3+…+n）²．
分析：（1）通过计算判断大小．
（2）根据所给图形的面积证明（1）的判断．
（3）根据以上两个题的计算和验证结论来推导．
点评：解决本题的关键是根据所给图形的面积间的关系来推导出公式．