
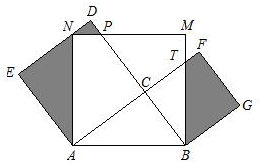
 直角三角形ABC的两直角边AC=8cm,BC=6cm,以AC、BC为边向形外分别作正方形ACDE与BCFG,再以AB为边向上作正方形ABMN,其中N点落在DE上,BM交CF于点T.问:图中阴影部分(△ANE、△NPD与梯形BTFG)的总面积等于多少?
直角三角形ABC的两直角边AC=8cm,BC=6cm,以AC、BC为边向形外分别作正方形ACDE与BCFG,再以AB为边向上作正方形ABMN,其中N点落在DE上,BM交CF于点T.问:图中阴影部分(△ANE、△NPD与梯形BTFG)的总面积等于多少?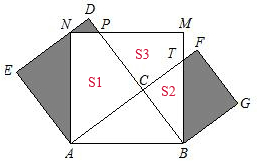


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:小学数学 来源: 题型:
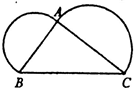 如图,以直角三角形ABC的两条直角边为直径作两个半圆,己知这两段半圆弧的长度之和是37.68厘米,那么三角形ABC的面积最大是
如图,以直角三角形ABC的两条直角边为直径作两个半圆,己知这两段半圆弧的长度之和是37.68厘米,那么三角形ABC的面积最大是查看答案和解析>>
科目:小学数学 来源: 题型:
 图中,直角三角形ABC 的两条直角边AB 和BC 的长度分别为3和4,将三角形ABC绕点C顺时针旋转至A1B1C,使得A1C与B1C在直线l上.
图中,直角三角形ABC 的两条直角边AB 和BC 的长度分别为3和4,将三角形ABC绕点C顺时针旋转至A1B1C,使得A1C与B1C在直线l上.| AD | A1D |
查看答案和解析>>
科目:小学数学 来源: 题型:
 直角三角形ABC中,∠ABC=90.,AB=20厘米,以AB为直径的半圆与直角三角形ABC的重叠部分用阴影表示,不重叠的两部分甲和乙,甲的面积比乙的面积大75平方厘米,求直角边BC的长.
直角三角形ABC中,∠ABC=90.,AB=20厘米,以AB为直径的半圆与直角三角形ABC的重叠部分用阴影表示,不重叠的两部分甲和乙,甲的面积比乙的面积大75平方厘米,求直角边BC的长.查看答案和解析>>
科目:小学数学 来源: 题型:填空题
 如图,以直角三角形ABC的两条直角边为直径作两个半圆,己知这两段半圆弧的长度之和是37.68厘米,那么三角形ABC的面积最大是________平方厘米(π取3.14).
如图,以直角三角形ABC的两条直角边为直径作两个半圆,己知这两段半圆弧的长度之和是37.68厘米,那么三角形ABC的面积最大是________平方厘米(π取3.14).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com