
分析 把甲杯中原有水量看作单位“1”,通过几次计算发现规律,倒的次数为奇数次的时候,两杯中的水一样多.因为2015是奇数,故这时甲杯中的水与乙杯中水一样多,均为$\frac{1}{2}$,所以甲杯中的水是原来的$\frac{1}{2}$.
解答 解:设甲杯中原有水为单位“1”,则甲、乙两杯的总量也为“1”,乙的量=1-甲的量;
第1次倒出的量为:1×$\frac{1}{2}$=$\frac{1}{2}$,第1次倒后:甲=$\frac{1}{2}$,乙=1-$\frac{1}{2}$=$\frac{1}{2}$;
第2次倒出的量为:$\frac{1}{2}$×$\frac{1}{3}$=$\frac{1}{6}$,第2次倒后:甲=$\frac{1}{2}$+$\frac{1}{6}$=$\frac{2}{3}$,乙=1-$\frac{2}{3}$=$\frac{1}{3}$;
第3次倒出的量为:$\frac{2}{3}$×$\frac{1}{4}$=$\frac{1}{6}$,第3次倒后:甲=$\frac{2}{3}$-$\frac{1}{6}$=$\frac{1}{2}$,乙=1-$\frac{1}{2}$=$\frac{1}{2}$;
第4次倒出的量为:$\frac{1}{2}$×$\frac{1}{5}$=$\frac{1}{10}$,第4次倒后:甲=$\frac{1}{2}$+$\frac{1}{10}$=$\frac{3}{5}$,乙=1-$\frac{3}{5}$=$\frac{2}{5}$;
第5次倒出的量为:$\frac{3}{5}$×$\frac{1}{6}$=$\frac{1}{10}$,第5次倒后:甲=$\frac{3}{5}$$-\frac{1}{10}$=$\frac{1}{2}$,乙=1-$\frac{1}{2}$=$\frac{1}{2}$;
可得:倒的次数为奇数次的时候,两杯中的水一样多均为$\frac{1}{2}$,
因为2015是奇数,所以倒2015次后,甲杯中的水是原来的$\frac{1}{2}$.
答:反复倒2015次后,甲杯中的水是原来的$\frac{1}{2}$.
点评 解答本题的关键是通过几次计算发现规律,并能用规律解答问题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
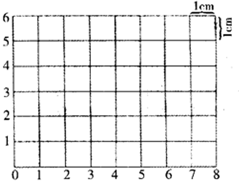 (1)在方格图中,画一个圆,圆心O的位置是(6,4),圆的半径是2cm.
(1)在方格图中,画一个圆,圆心O的位置是(6,4),圆的半径是2cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com