
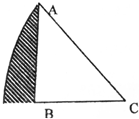
 一个等腰直角三角形ABC的面积是20平方厘米,阴影部分的面积是多少?
一个等腰直角三角形ABC的面积是20平方厘米,阴影部分的面积是多少? 分析  根据图形可得:阴影部分的面积=这个$\frac{1}{4}$圆的面积-正方形ABCD的面积,连接正方形的对角线AC,BD,根据正方形的对角线的特点可得:AO=CO=BO=OD=半径的一半,得到四个全等的直角三角形,三角形ABC的面积已知,于是可以求出圆的半径的平方值,于是问题即可得解.
根据图形可得:阴影部分的面积=这个$\frac{1}{4}$圆的面积-正方形ABCD的面积,连接正方形的对角线AC,BD,根据正方形的对角线的特点可得:AO=CO=BO=OD=半径的一半,得到四个全等的直角三角形,三角形ABC的面积已知,于是可以求出圆的半径的平方值,于是问题即可得解.
解答 解:据分析可得:
设圆的半径为r,
则$\frac{r}{2}$×$\frac{r}{2}$×$\frac{1}{2}$×4=20×2
$\frac{{r}^{2}}{4}$=20
r2=80
所以阴影部分的面积为:
$\frac{1}{2}$×(3.14×80×$\frac{1}{4}$-20×2)
=$\frac{1}{2}$×(62.8-40)
=11.4(平方厘米)
答:阴影部分的面积是11.4平方厘米.
点评 本题主要考查组合图形的面积,求出圆的半径的平方值,是解答本题的关键.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com