
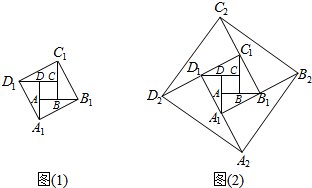
分析 本题需先根据已知条件得出延长n次时面积的公式,再根据求正方形A4B4C4D4正好是要求的第5次的面积,把它代入即可求出答案.在直角三角形CC1中,CD1=2,CC1=1,运用勾股定理可求得C1D1=$\sqrt{5}$,所以延长一次为$\sqrt{5}$,面积为5,再延长为51=5,面积52=25,…,据此解答即可.
解答 解:最初边长为1,面积为1,
在直角三角形CC1中,CD1=2,CC1=1,
则(C1D1)2=(CC1)2+(CD1)2
=12+22
=1+4
=5
C1D1=$\sqrt{5}$,
所以延长一次为$\sqrt{5}$,面积为5,
再延长为51=5,面积52=25,…,
下一次延长为5$\sqrt{5}$,面积53=125,
以此类推,
当N=4时,正方形A4B4C4D4的面积为:54=625.
答:正方形A4B4C4D4的面积为625.
点评 本题主要考查了正方形的性质,在解题时要根据已知条件找出规律,从而得出正方形的面积,这是一道常考题.


科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
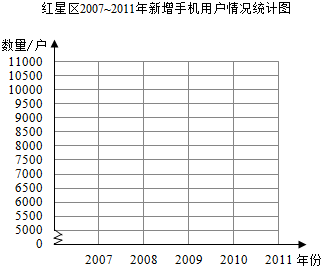
| 年份 | 2007 | 2008 | 2009 | 2010 | 201 |
| 数量/户 | 5500 | 6800 | 10500 | 9000 | 8000 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com