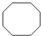
考点:数与形结合的规律
专题:探索数的规律
分析:(1)根据图示,可得第1个图形需要8根小棒,第2个图形需要15根小棒(15=8+7),第3个图形需要22根小棒(22=8+7×2),所以从第二个图形开始,每个图形都比它前面的图形多用7根小棒,据此求出第5个图形需要多少根小棒;
(2)根据图示,可得第2个图形等于14(14=15-1)根小棒的长度,第3个图形等于20(20=22-2)根小棒的长度,第4个图形等于26(26=29-3)根小棒的长度,…,据此求出第十个图形由多少根小棒组成,进而求出它的周长是多少厘米即可.
解答:
解:(1)根据图示,可得
第1个图形需要8根小棒,
第2个图形需要15根小棒(15=8+7),
第3个图形需要22根小棒(22=8+7×2),
所以从第二个图形开始,每个图形都比它前面的图形多用7根小棒,
所以第5个图形需要小棒的数量是:
8+7×4
=8+28
=36(根)
(2)由(1)可得,第10个图形需要小棒的数量是:
8+7×9
=8+63
=71(根)
根据图示,可得
第2个图形的周长等于14(14=15-1)根小棒的长度,
第3个图形的周长等于20(20=22-2)根小棒的长度,
第4个图形的周长等于26(26=29-3)根小棒的长度,
…,
所以第n个图形的周长等于组成它需要小棒的长度减去n-1个的小棒的长度,
所以第十个图形的周长是:
(71-9)×1
=62×1
=62(厘米)
答:第5个图形需要36根小棒、第十个图形周长是62厘米.
故答案为:36、62.
点评:此题主要考查了数形结合的规律问题的应用,注意观察总结出规律并能正确应用.