练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情

    【题目】如图，在三角形ABC中，已知三角形ADE、三角形DCE、三角形BCD的面积分别是89、26、28，那么三角形DBE的面积是　 　．

    【答案】6

    【解析】

    试题分析：根据题干分析，利用高一定时，三角形的面积与高成正比的性质可得：所以AD：DC=89：26；由此根据三角形BCD的面积是28，可以求得三角形ABD的面积，再减去三角形ADE即可得出三角形DBE的面积．

    解：已知三角形ADE、三角形DCE的面积分别是89、26，

    根据高一定时，三角形的面积与高成正比的性质可得：AD：DC=89：26；

    所以三角形ABD：三角形BCD的面积=89：26，又因为三角形BCD=28，

    所以三角形ABD的面积是：89×28÷26=95，

    则三角形DBE的面积为：95﹣89=6，

    答：三角形DBE的面积是6，

    故答案为：6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

    【题目】如果a是2的倍数，2是a的因数，那么a+1的和一定是奇数．　 　．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    【题目】3个十和7个一是（______）。

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    【题目】六（1）班有a人，比六（2）班的2倍少b人，用含有字母的式子表示六（2）班的人数是（　　）

    A.2a+b B.（a﹣b）÷2 C.a÷2﹣b D.（a+b）÷2

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    【题目】a÷b=c…7，若a与b同时缩小10倍，则余数是（　　）

    A.70 B.7 C.0.7 D.0.07

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    【题目】四位数除以两位数，商可能是三位数，也可能是两位数．　 　．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：

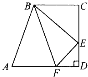
    【题目】右面的直角梯形中，已知梯形上底6cm，下底9cm，高8cm，三角形ABF、三角形BCE和四边形BEDF面积相等，三角形BEF的面积是　 　cm2．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    【题目】48÷6=□×2，□里填8．　 　．（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    【题目】甲数是乙数的4倍，甲数与乙数的比是　 　；如果甲数是乙数的40%，甲数与乙数的比是　 　．

    查看答案和解析>>

    同步练习册答案