Question

如图所示，摆放小正方体．
（1）当摆到第七层时一共有

 

个小正方体．
（2）当摆放到n层时一共

 

个正方体．

Answer 1

考点：数与形结合的规律

专题：探索数的规律

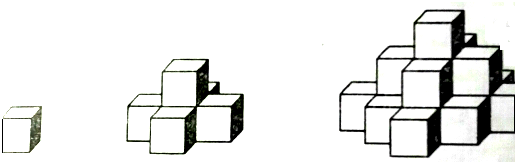
分析：图（1）中只有一层，有（4×0+1）一个正方形，图（2）中有两层，在图（1）的基础上增加了一层，第二层有（4×1+1）个．图（3）中有三层，在图（2）的基础长增加了一层，第三层有（4×2+1），依此类推当图形有二层和七层时总的正方形的个数．
依此类推总结规律当有n层时总的正方体个数．

解答： 解：根据分析：当图形有二层时，第二层的正方形个数为：（4×1+1），则此时总的正方形个数为1+（4×1+1）=6；
当图形有七层时，第七层的个数为：（4×6+1），
则此时总的正方形个数为：1+（4×1+1）+（4×2+1）+（4×3+1）+（4×4+1）+（4×5+1）+（4×6+1）=91．
归纳可知，第n个叠放图形中共有n层，构成了以1为首项，以4为公差的等差数列
所以S_n=n+

n(n-1)×4

=2n²-n
故答案为：91，2n²-n．

点评：本题主要考查归纳推理，其基本思路是先分析具体，观察，总结其内在联系，得到一般性的结论，若求解的项数较少，可一直推理出结果，若项数较多，则要得到一般求解方法，再求具体问题．