Question

19．如图，已知三角形AOD的面积为4平方厘米，三角形DOC的面积为10平方厘米．求梯形ABCD的面积．

Answer 1

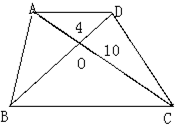
分析 首先根据三角形的面积和底的正比关系，求出AO、CO的比是多少；然后根据AD∥BC，可得$\frac{DO}{BO}=\frac{AO}{CO}$，再根据三角形的面积和底的正比关系，分别求出三角形AOB的面积、三角形BOC的面积各是多少，进而求出梯形ABCD的面积是多少即可．

解答 解：因为S_△AOD：S_△DOC=4：10=2：5，
所以$\frac{AO}{C0}=\frac{2}{5}$，
因为AD∥BC，
所以$\frac{DO}{BO}=\frac{AO}{CO}$=$\frac{2}{5}$，
所以${S}_{△AOB}={\frac{5}{2}S}_{△AOD}$=$\frac{5}{2}×4=10$（平方厘米），
所以${S}_{△BOC}={\frac{5}{2}S}_{△DOC}=\frac{5}{2}×10=25$（平方厘米），
所以S_梯形ABCD=S_△AOD+S_△DOC+S_△AOB+S_△BOC
=4+10+10+25
=49（平方厘米）
答：梯形ABCD的面积是49平方厘米．

点评 此题主要考查了三角形的面积和底的正比关系的应用，要熟练掌握，解答此题的关键是分别求出三角形AOB的面积、三角形BOC的面积各是多少．