Question

16．如图：梯形面积为45平方米，高6米，三角形AED的面积为5平方米，求阴影部分面积．

Answer 1

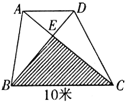
分析 根据梯形的面积公式先求出梯形的上底，即AD=45×2÷6-10=5厘米，因为△ADE和△BCE是相似三角形，三角形面积的比等于相似比的平方，所以S_△ADE：S_△BCE=AD²：BC²=5²：10²，再根据三角形AED的面积为5平方米，即可求出阴影部分面积．

解答 解：AD=45×2÷6-10=5（厘米），
因为△ADE和△BCE是相似三角形，三角形面积的比等于相似比的平方，
所以，S_△ADE：S_△BCE=AD²：BC²=5²：10²=1：4，
所以，S_△BCE=5×4=20（平方厘米）
答：阴影部分面积的面积是20平方厘米．

点评 本题考查了相似三角形的性质的灵活应用，关键是明确相似三角形面积的比等于相似比的平方，本题体现了数形结合的规律．