
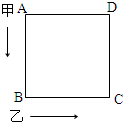
 如图,甲、乙两人沿着边长为90米的正方形,按A→B→C→D→A…方向,甲从A以65米/分的速度,乙从B以72米/分的速度同时行走,当乙第一次追上甲时在正方形的( )
如图,甲、乙两人沿着边长为90米的正方形,按A→B→C→D→A…方向,甲从A以65米/分的速度,乙从B以72米/分的速度同时行走,当乙第一次追上甲时在正方形的( )| A、AB边上 | B、DA边上 | C、BC边上 | D、CD边上 |
| 4 |
| 7 |
| 4 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 81 |
| 84 |
| 3 |
| 4 |
| 81 |
| 84 |
| 270 |
| 7 |
| 81 |
| 84 |
| 3 |
| 4 |
| 81 |
| 84 |


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:小学数学 来源: 题型:
 如图,ABCD是边长为10米的正方形,甲从A、乙从D同时开始按逆时针方向沿着正方形的边行走,甲的速度是乙速度的4倍,当甲、乙两人第一次距离(直线距离)最远时,甲行走的路程是
如图,ABCD是边长为10米的正方形,甲从A、乙从D同时开始按逆时针方向沿着正方形的边行走,甲的速度是乙速度的4倍,当甲、乙两人第一次距离(直线距离)最远时,甲行走的路程是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com