考点:组合图形的计数
专题:几何的计算与计数专题
分析:
观察图形可知,以A、B为顶点的三角形有7个;
以A、C为顶点的三角形有3个;
以A、D为顶点的三角形有2个;
以A、E为顶点的三角形有1个;
以A、F为顶点的三角形有3个;
以A、G为顶点的三角形有2个;
以A、H为顶点的三角形有3个;
以A、I为顶点的三角形有1个;
以A、J为顶点的三角形有5个;
以A、K为顶点的三角形有4个;
以A、L为顶点的三角形有2个;
以A、M为顶点的三角形有2个;
以A、N为顶点的三角形有1个;
以B、C为顶点的三角形有1个;
以B、D为顶点的三角形有1个;
以B、E为顶点的三角形有1个;
以B、F为顶点的三角形有1个;
以B、J为顶点的三角形有1个;
以C、F为顶点的三角形有1个;
以D、F为顶点的三角形有1个;
以E、F为顶点的三角形有1个;
以F、K为顶点的三角形有1个;
以G、H为顶点的三角形有1个;
以G、K为顶点的三角形有1个;
以H、I为顶点的三角形有1个;
以H、K为顶点的三角形有3个;
以I、K为顶点的三角形有1个;
JN下面的三角形有4+3+2+1=10,相加即可求解.
解答:
解:由分析可知,
(7+3+2+1+3+2+3+1+5+4+2+2+1)+1×5+1+1+1+1+1×2+(1+3)+1+(4+3+2+1)
=36+5+4+2+4+1+10
=62(个).
答:图中共有62个三角形.
故答案为:62.
点评:此题主要考查了计数方法的应用,根据不同的顶点分别列举得出是解题的关键.

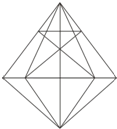
 观察图形可知,以A、B为顶点的三角形有7个;
观察图形可知,以A、B为顶点的三角形有7个;
