
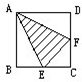
 正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于________平方厘米.
正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于________平方厘米. ×(3.6×8+2.8×8+4.4×5.2)=37.04(平方厘米);所以阴影部分的面积=8×8-37.04=26.96(平方厘米).
×(3.6×8+2.8×8+4.4×5.2)=37.04(平方厘米);所以阴影部分的面积=8×8-37.04=26.96(平方厘米). ×(3.6×8+2.8×8+4.4×5.2),
×(3.6×8+2.8×8+4.4×5.2), ×(28.8+22.4+22.88),
×(28.8+22.4+22.88), ×74.08,
×74.08,

 阅读快车系列答案
阅读快车系列答案科目:小学数学 来源: 题型:

查看答案和解析>>
科目:小学数学 来源: 题型:
 奥运会即将开幕了,全市掀起了美化城市的热潮.有位同学为一家商店设计了一副霓虹灯闪烁的原理图.
奥运会即将开幕了,全市掀起了美化城市的热潮.有位同学为一家商店设计了一副霓虹灯闪烁的原理图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com