
 按要求操作
按要求操作分析 (1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可画出图形M.
(2)根据旋转的特征,图M绕点B顺时针旋转90°,点O的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形民N.
(3)根据平移的特征,把图N的各顶点分别向左平移4格,依次连结即可得到向左平移4格后的图形.
(3)图形M或看作是底为5毫米,高为2毫米的三角形,根据三角形面积计算公式“S=ah÷2”即可求出它的面积.
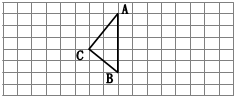
解答 解:(1)在左面的方格图中描出点A(8,7),B(8,2),C(6,4),连接ABC,得到图形M(下图):
(2)将图形M绕点B点顺时针旋转90°,得到新图形N(下图红色部分):
(3)将图形N向左平移4格(下图绿色部分):
(4)图形M的面积:
5×2÷2
=10÷2
=5(平方毫米).
点评 此题考查的知识有:数对与位置、作平移后的图形、作旋转一定度数后的图形、三角形面积的计算等.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:计算题
| $\frac{1}{6}+\frac{5}{6}$= | $\frac{3}{8}+\frac{1}{8}$= | 2.5+7.5= | 275-99= | $\frac{1}{2}-\frac{1}{3}$= | $\frac{6}{7}-\frac{4}{7}$= | 5.6×4= | 10-3.6= |
| $\frac{1}{4}+\frac{1}{5}$= | $\frac{7}{9}-\frac{1}{9}$= | 0.4×80= | 4.5×0.2= | 1-$\frac{2}{3}$= | $\frac{1}{4}+\frac{1}{12}$= | 6.9÷23= | 0.4÷5= |
| $\frac{7}{10}-\frac{1}{2}$= | 1+$\frac{4}{5}$= | 8.5÷17= | 12.98-2.98= | $\frac{1}{5}+\frac{1}{20}$= | $\frac{9}{10}-\frac{4}{5}$= | 3.9÷10= | 1÷25= |
| $\frac{5}{12}+\frac{6}{12}$= | $\frac{5}{7}+\frac{3}{7}$= | 728÷7= | 1.25×8= | $\frac{9}{8}$-1= | $\frac{7}{11}-\frac{7}{11}$= | 0×9.05= | 6.4+4.6= |
| 1-$\frac{1}{4}-\frac{1}{4}$= | 1$\frac{2}{3}$+1= | 6×0.4×2.5= | 3.5×8÷8= | 1-$\frac{1}{3}+\frac{1}{3}$= | 1+$\frac{7}{9}+\frac{1}{9}$= | 2.1÷0.7+7= | 0.2+0.2÷0.2= |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com