
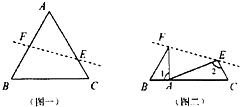 如图一,将等边三角形ABC沿直线EF对折(图一),使A点落在BC上(图二),请问图二中1,2所标示的两个角的度数之差为多少度?答案:0度.
如图一,将等边三角形ABC沿直线EF对折(图一),使A点落在BC上(图二),请问图二中1,2所标示的两个角的度数之差为多少度?答案:0度. 分析 三角形ABC是等边三角形,所以∠A=∠B=∠C=60°,因为三角形的内角和是180°,所以在三角形EAC中:∠2+∠EAC=180°-60°=120°,因为∠A=60°,所以∠1+∠EAC=180°-60°=120°,所以∠1=∠2,由此即可得出结论.
解答 解:三角形ABC是等边三角形,所以∠A=∠B=∠C=60°,
因为三角形的内角和是180°,所以在三角形EAC中:∠2+∠EAC=180°-60°=120°,
因为∠A=60°,所以∠1+∠EAC=180°-60°=120°,所以∠1=∠2,
所以∠1-∠2=0°;
故答案为:0.
点评 此题属于简单图形的折叠问题,推出:∠2+∠EAC=∠1+∠EAC=120°,是解答此题的关键.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题

查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 那么,当圆柱管有100个时需要绳子1608厘米(π取3)
那么,当圆柱管有100个时需要绳子1608厘米(π取3)查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com