考点:繁分数的化简
专题:计算问题(巧算速算)
分析:首先把分数
| 12×(12+22)×(12+22+32)×…×(12+22+…+1002) |
| 100! |
化简,然后分别找出分母、分子中因数2、3的个数,进而求出化成最简分数后的分母即可.
解答:
解:根据题意,可得
12=,
12+22=,
12+22+32=,…1
2+2
2+…+n
2=
,
所以
| 12×(12+22)×(12+22+32)×…×(12+22+…+1002) |
| 100! |
=
×××…×
×
=
| (1×2×…100)×(2×3×…×101)×(3×5×…×201) |
| 6100?100! |
=
| (2×3×…×101)×(3×5×…×201) |
| 6100 |
=
| (2×4×6×…×100)×(3×5×…×101)×(3×5×…×201) |
| 6100 |
分子中2×4×6×…×100含有97个因数2,22个因数3,
分子中3×5×7×…×101含有26个因数3,
分子中3×5×7×…×201含有50个因数3,
所以分子中一共含有97个因数2,98个因数3,分母中一共含有100个因数2,100个因数3,
因此分子、分母约分后分母还有3个因数2,2个因数3,
由2×2×2×3×3=72,
可得分数
| 12×(12+22)×(12+22+32)×…×(12+22+…+1002) |
| 100! |
化成最简分数后的分母是72.
点评:此题主要考查了繁分数的化简的应用,解答此题的关键是求出分母、分子中因数2、3的个数.



 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案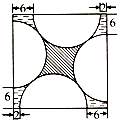 如图,在一个正方形中恰好放了四个相同的半圆,每个半圆的直径恰好都在边上,一些线段的长度如图所示,那么中间的阴影面积与四个角上的阴影面积之差是多少?(л取3.14)
如图,在一个正方形中恰好放了四个相同的半圆,每个半圆的直径恰好都在边上,一些线段的长度如图所示,那么中间的阴影面积与四个角上的阴影面积之差是多少?(л取3.14)