
分析 三个自然数的百位数字都是1,由于中间的数能被5整除,故中间数的个位数字只能是0或5,从而最小的数的末位数字只能是9或4(即10-1=9,5-1=4);下一步可利用被3整除的数的特征确定其十位数字,最后再用牧举法确定这3个连续整数即可.
解答 解:这三个连续整数在100-200之间,故其百位数字确定为1.由于中间数能被5整除,故其末位数为0或5,
所以,最小数的百位数字为1,个位数字为9或4;
若最小数的个位数字为9,由其能被3整除,故其十位数字为2、5、8;
若最小数的个位数字围,由其能被三整除,其十位数字为1,4,7;
从而,最小数只可能是129,159,189,114,144,174中的某几个数130,160,190,115,145,175已能被5整除,故只须从131,161,191,116,146,176中筛选出能被7整除的数,
即:上述六数中只有161=7×23满足要求;
所以所求连续三数为159,160,161;
故答案为:159,160,161.
点评 根据能被5整除的数的特征得出中间数的个位数字只能是0或5,最小的数的末位数字只能是9或4,是解答此题的关键所在.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
| 107+199= | 1-0.9= | 2.5×0.4= | 3.6÷12= |
| $\frac{3}{11}$$÷\frac{3}{8}$= | 1-$\frac{4}{9}$+$\frac{5}{9}$= | $\frac{3}{4}$×3÷$\frac{3}{4}$= | ($\frac{1}{2}$+$\frac{1}{3}$)×6= |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
| $\frac{1}{5}$+$\frac{3}{5}$= | $\frac{2}{3}$-$\frac{1}{4}$= | $\frac{5}{8}$×$\frac{4}{5}$= | $\frac{9}{20}$÷$\frac{3}{10}$= |
| 2.5×0.4= | 60÷1.5= | 120×10%= | 383-299= |
查看答案和解析>>
科目:小学数学 来源: 题型:选择题
| A. | 24 | B. | 20 | C. | 18 | D. | 16 |
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
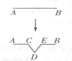 对于一个多边形,定义一种“生长”操作(如图),将其中一边AB变成折线ACDEB,其中C和E是AB的三等分点,C、D、E三点可构成等边三角形,那么,一个边长是9的等边三角形,经过四次“生长”操作得到的图形的周长是85$\frac{1}{3}$.
对于一个多边形,定义一种“生长”操作(如图),将其中一边AB变成折线ACDEB,其中C和E是AB的三等分点,C、D、E三点可构成等边三角形,那么,一个边长是9的等边三角形,经过四次“生长”操作得到的图形的周长是85$\frac{1}{3}$.查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com