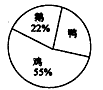Question

数一数，下图分别有多少个三角形？

你发现了什么规律吗？说说看．

Answer 1

分析：图1有2个小三角形和1个大三角形，一共是2+1=3个三角形；
图2有3个小三角形，每两个小三角形又可以组成2个三角形，再有1个大三角形，共有3+2+1=6个三角形；
图3有4个小三角形，每两个小三角形又可以组成3个三角形，每3个三角形又组成2个三角形，再有1个大三角形，共有4+3+2+1=10个三角形；
图4有5个小三角形，每两个小三角形又可以组成4个三角形，每3个三角形又组成3个三角形，每4个小三角形可以组成2个三角形；再有1个大三角形，共有5+4+3+2+1=15个三角形；由此得出规律：图形中的小三角形个数为n，则图中三角形的总个数就是：1+2+3+4+5+…+n．

解答：解：图1有2个小三角形，共有2+1=3个三角形；
图2有3个小三角形，共有3+2+1=6个三角形；
图3有4个小三角形，共有4+3+2+1=10个三角形；
图4有5个小三角形，共有5+4+3+2+1=15个三角形；
由此得出规律：图形中的小三角形个数为n，则图中三角形的总个数就是1+2+3+4+…+n．

点评：此题解答的关键是：一定要认真观察，有条理、有顺序的先进行数数；再去找规律即可．