
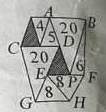
 如图,AB,CD,EF,GH两两平行且AB=CD=EF=GH,图中每个数字表示其所在三角形的面积,图中两个阴影三角形的面积和是多少?
如图,AB,CD,EF,GH两两平行且AB=CD=EF=GH,图中每个数字表示其所在三角形的面积,图中两个阴影三角形的面积和是多少? 分析 根据三角形面积公式,可以发现三角形ABP和三角形CDG的底和高都相同,从而得出两个阴影部分三角形的高相同,根据三角形ABP和三角形BPF的面积得出PF和AB之间的关系,再根据可以得出它的高和三角形ABP的关系,所以可以设三角形ABP的高为h,底为a,三角形EFH的高为h1,从而得出ah=40,PF=$\frac{3}{10}$a,EP=$\frac{7}{10}$a,h1=$\frac{2}{5}$h,则三角形DEP的高为$\frac{3}{5}$h,再根据面积是5的三角形,可得底是$\frac{5}{8}$a,上面阴影的底是$\frac{3}{8}$a,两个阴影的底和高都知道了,从而可求面积和.
解答 解:设三角形ABP的高为h,底为a,三角形EFH和上面阴影三角形的高都为h1,
根据题意有$\frac{1}{2}$ah=20
所以ah=40
因为三角形BPF的面积是6,
所以$\frac{1}{2}$PF×h=6
从而PF=$\frac{2}{5}$a,EP=$\frac{3}{5}$a
因为三角形EFH的面积是8,
所以$\frac{1}{2}$ah1=8
从而h1=$\frac{2}{5}$h,三角形DEP的高为$\frac{3}{5}$h
所以三角形DEP的面积为$\frac{1}{2}$×$\frac{3}{5}$a×$\frac{3}{5}$h=$\frac{9}{50}$ah=$\frac{9}{50}$×40=7.2
设面积为5的三角形的底为a1
则有:$\frac{1}{2}$a1$\frac{2}{5}$h=5
得出a1=$\frac{5}{8}$a
从而上面阴影的底为$\frac{3}{8}$a
所以上面阴影的面积为:$\frac{1}{2}$×$\frac{3}{8}$a×$\frac{2}{5}$h=$\frac{3}{40}$ah=3
所以阴影面积的和是7.2+3=10.2
答:图中两个阴影三角形的面积和是10.2.
点评 解答本题的关键是掌握三角形面积公式,根据题目给的条件找到两个阴影三角形的底和高与已知三角形底和高之间的关系.


科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题

查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com