考点:数与形结合的规律
专题:探索数的规律
分析:(1)搭一个三角形需3根火柴,搭2个三角形中间少用1根,需要5根火柴棒,搭3个三角形中间少用2根,需要7根火柴棒,搭4个三角形中间少用3根,需要9根火柴棒…搭n个三角形中间少用(n-1)根,需要[3n-(n-1)]=2n+1根火柴棒.
(2)摆1个六边形需要6根小棒,可以写作:5×1+1;摆2个需要11根小棒,可以写作:5×2+1;摆3个需要16根小棒,可以写成:5×3+1;…由此可以推理得出一般规律解答问题.
(3)摆一个八边形用了8根小棒,摆两个八边形就多用了7根,摆三个就多用了7×2根,…能够根据图形发现规律:多一个八边形,就多用7根小棒,则在第n个图形中,需要小棒:8+7(n-1)=7n+1根.
解答:
解:(1)搭一个三角形需3根火柴
搭2个三角形中间少用1根,需要5根火柴棒
搭3个三角形中间少用2根,需要7根火柴棒
搭4个三角形中间少用3根,需要9根火柴棒
…,
所以搭n个三角形中间少用(n-1)根,需要[3n-(n-1)]=2n+1根火柴棒.
(2)解:根据题干分析可得:摆1个六边形需要6根小棒,可以写作:5×1+1;
摆2个需要11根小棒,可以写作:5×2+1;
摆3个需要16根小棒,可以写成:5×3+1;…
摆n个六边形需要:5n+1根小棒,
(3)根据题干分析可得:在第n个图形中,需要小棒8+7(n-1)=7n+1根.
故答案为:2n+1;5n+1;7n+1.
点评:根据题干中已知的图形的排列特点及其数量关系,推理得出一般的结论进行解答,是此类问题的关键.

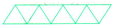 …摆n个这样的三角形需要
…摆n个这样的三角形需要 …摆n个这样的六边形需要
…摆n个这样的六边形需要 …摆n个这样的八边形需要
…摆n个这样的八边形需要

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案