考点:竖式数字谜
专题:填运算符号、字母等的竖式与横式问题
分析:(1)由于和的最高位是5,故此可得:我可能是4或5,当我是5时,5+9=14,和的最高位不会是5,故我=4;那么要就有可能是8或9,当要=9时,4+9=13,由于和的十位是3,要想满足算式需要十位的和想百位进一,也就是说学=0,但是根据算式可得:找不到满足竖式的数,据此要=8;当要=8时,4+8=12,那么学就可能7,8或9,由于不能重复,那么学就该是7或9,当学是7时,4+8+7=19,要想等式成立,找不到满足竖式的好的值,据此可得学=9,当学=9时,好=1,代入竖式可得算式成立,据此即可解答.
(2)根据E+E=E可得:E=0,再根据一个四位数加一个四位数的和是五位数可得:A=1;由于和的千位是0,当A=1时,B应该是8或9,当B=8时,依据和的十位是8,A=1可得:C=7,但C=7时,找不到D的值,据此B=9;根据9-1=8可得:C=8;8÷2=4,所以D=4;据此即可解答.
解答:
解:

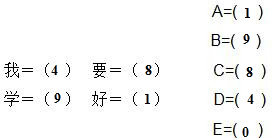
.
点评:本题考查学生的加法的计算熟练程度,能激起学生学习的兴趣,是个好题.



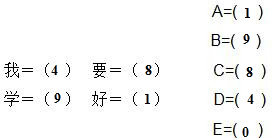 .
.

