周长相等的长方形、正方形、圆,它们的面积中,圆的面积大.
正确
分析:我们采用假设的方法解答这道题,假设周长是16厘米,进而求得长方形和正方形的面积、圆的面积,进行比较得出结论.
解答:为了便于理解,假设正方形、长方形和圆形的周长都是16,
则圆的半径为:
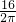
=
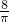
,π×
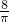
×
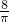
=
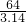
=20.38;
正方形的边长为:16÷4=4,面积为:4×4=16;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:5×3=15,
当长方形的长和宽最接近时面积也小于16;
所以周长相等的正方形、长方形和圆形,圆面积最大.
故答案为:正确.
点评:此题没有数据,分析时应假设出周长,然后根据面积公式进行分析,进而得出问题答案;可以得出结论:周长相等的长方形、正方形和圆,圆的面积最大,正方形其次,长方形的面积最小.

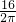 =
=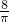 ,π×
,π×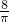 ×
×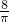 =
=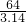 =20.38;
=20.38;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案