
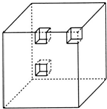
 如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,挖掉的小立方体的棱长是________厘米.
如图,有一个边长为20厘米的大正方体,分别在它的角上、棱上、面上各挖掉一个大小相同的小立方体后,表面积变为2454平方厘米,挖掉的小立方体的棱长是________厘米.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:小学数学 来源: 题型:
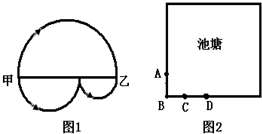 一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).
一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).
一个农民牵着一头牛从甲地到乙地去放牧,从甲地到乙地有两条路,第一条路是一个大半圆,第二条路是两个不同小半圆(如图1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com