考点:筛选与枚举,排列组合
专题:传统应用题专题
分析:根据题意,买4份麦当劳,不看钱数,可以分为:A类1份和B类3份;A类2份和B类2份;A类3份和B类1份;A类4份;B类4份;共5种买法,但是要考虑他所带的钱数,也就是花的钱数不能超过所带的钱数,然后再进一步解答即可.
解答:
解:根据题意可得:
第一种:A类1份和B类2份,花的钱数是:18+21×3=81(元)>80,不合题意;
第二种:A类2份和B类2份,花的钱数是:18×2+21×2=78(元)<80,符合题意;
第三种:A类3份和B类1份,18×3+21=75(元)<80,符合题意;
第四种:A类4份,花的钱数是:18×4=72(元)<80,符合题意;
第五种:B类4份,花的钱数是:21×4=84(元)>80,不合题意.
由以上分析可得,他一共有3种买法.
答:有3种买法.
故答案为:3.
点评:根据题意,只分析有几种买法非常简单,而本题所带的钱数只有80元,那么在所有的买法中,花掉的钱数不能超过80元,假如超过80元了,那么此种买法就不存在.

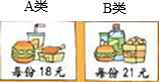 是“麦当劳”两种套餐的价格,带80元钱买4份,有
是“麦当劳”两种套餐的价格,带80元钱买4份,有
