练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    1．在1～50的自然数中所有不能被3整除的数的和是多少？

    分析 用1至50以内所有整数的和减去所有能被3整除的数的和，就是所有不能被3整除的数的和；据此先求出1～50这50个数的和，再求出50以内所有能被3整除的数的和（各个数位上的数的和是3的倍数），以上二和之差就是所有不能被3整除的数的和，列式解答即可．

    解答 解：1～50这50个数的和：1+2+3+4+5+6+…50
    =（50+1）×50÷2
    =51×50÷2
    =1275；
    50以内所有能被3整除的数的和：
    3+6+9+12+15+15+…+48
    =（3+48）×16÷2
    =51×8
    =408
    50以内所有不能被3整除的数的和：
    1275-408=867
    答：在1～50的自然数中所有不能被3整除的数的和是867．

    点评 解决此题关键是先求出1～50这50个数的和与50以内所有能被3整除的数的和，进一步求出所有不能被3整除的数的和．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：填空题

    11．若x=y，则$\frac{1}{2}$x+5=$\frac{1}{2}$y-5．×（判断对错）

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    12．下面是王老师调查并整理的三（一）同学最喜欢的动画片统计表．
    三（一）班同学最喜欢的动画片统计表
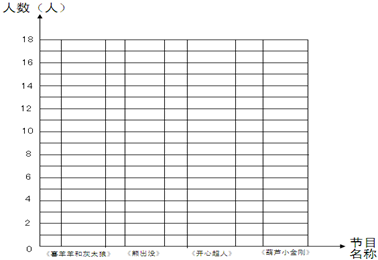
    节目名称《喜羊羊和灰太狼》《熊出没》《开心超人》《葫芦小金刚》
    人数（人）1613811
    （1）根据上面的统计表，完成统计图．
    三（一）班同学最喜欢的电视节目统计图

    （2）三（一）班同学最喜欢动画片《熊出没》的人比最喜欢《开心超人》的人多5，三（一）班一共有48人．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    9．四年级（1）班男、女生分别分成三组进行跳远比赛，得分情况如下表．
       组别  
        得分    
    队别    		一二三
    男生队1086
    女生队队81210
    根据得分统计表完成下面统计图．
    四（1）班男、女生队三个组别跳远比赛得分情况统计图

    （1）男生队第一组得分最高，第三组得分最低，三个组共得24分．
    （2）女生队第一组得分最低，最高与最低积分相差4分．
    （3）男生队平均每组得8分，女生队平均每组得10分，此次比赛二队获胜．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    16．-次学生就餐活动，学生每人用一只碗盛饭，每两人合用3碗菜，每三人合用2碗汤，结果共用碗95只．参加活动的学生共有多少名？

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    6．城关炼钢厂10月份上旬炼钢的重量占全月产量的$\frac{1}{5}$、中旬炼钢的重量占全月产量的$\frac{2}{5}$，下旬炼钢$\frac{3}{10}$万吨．这个厂10月份炼钢多少万吨？（用方程解）

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    13．一个数的$\frac{2}{5}$是46，它的60%是69．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    10．如图所示，半圆的直径为8厘米，求阴影部分的面积．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    11．三条边分别是4厘米、4厘米、6厘米的三角形是一个等腰三角形．√．（判断对错）

    查看答案和解析>>

    同步练习册答案