分析:为了便于好看加上了如下字母,(1)以A为顶点AB为一条边共有三角形4+3+2+1=10(个),然后再以A为顶点AC为一条边共有三角形4+3+2+1=10(个),以A为顶点AD为一条边共有三角形4+3+2+1=10(个),以A为顶点AE为一条边共有三角形4+3+2+1=10(个);(2)以B为顶点的三角形:即三角形BFC,三角形BFD和三角形BFE共3个;分别以G,H,I为顶点的三角形各有3个,由此可知以线段BF上的点为顶点的三角形以线段三角形共3×4=12个.(3)同上以线段CF上的点为顶点的三角形共2×4=8个;(4)以线段DF上的点为顶点的三角形共1×4=4个.
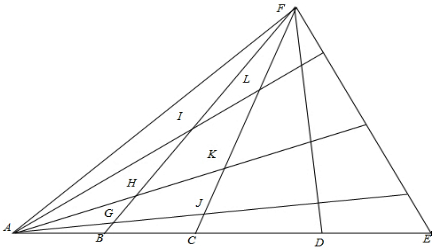
解答:解:(1)(4+3+2+1)×4+3×4+2×4+1×4
=10×4+12+8+4
=64(个)
故答案为:64.
点评:要有规律、有次序地来数图中的三角形,既不能重复,又不能遗漏.所以关键在于寻找计数的规律,学会一些有顺序地思考问题的方法.