Question

求下面各图中阴影部分的面积．（单位：厘米）

Answer 1

考点：组合图形的面积

专题：平面图形的认识与计算

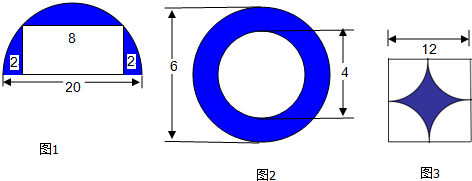
分析：（1）阴影部分的面积=半圆的面积-长方形的面积，圆的直径是20厘米，长方形的长和宽分别是8厘米和2厘米．
（2）阴影部分的面积等于外圆直径6厘米、内圆直径4厘米的圆环的面积，据此利用圆环的面积=π（R²-r²）计算即可解答．
（3）正方形内的空白部分可构成一个圆，因此，阴影面积=正方形的面积-圆的面积．

解答： 解：（1）3.14×（20÷2）²÷2-8×2
=3.14×100÷2-16
=157-16
=141（平方厘米）
答：阴影部分的面积是141平方厘米．

（2）3.14×[（6÷2）²-（4÷2）²]
=3.14×[9-4]
=3.14×5
=15.7（平方厘米）
答：阴影部分的面积是15.7平方厘米．

（3）12×12-3.14×（12÷2）²
=144-3.14×36
=144-113.04
=30.96（平方厘米）
答：阴影部分的面积是30.96平方厘米．

点评：解答此题的关键是弄清楚：阴影部分的面积可以由哪些图形的面积和或差求解．