Question

求下面图中阴影部分的面积．（单位：米）

Answer 1

考点：组合图形的面积

专题：平面图形的认识与计算

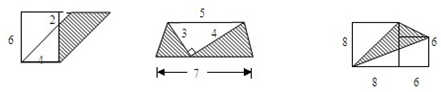
分析：（1）图中阴影部分是一个平行四边形减去下面的小直角三角形的面积即可．
（2）运用三角形面积公式先求出三角形的高，即3×4÷5，也就是梯形的高，用梯形面积减去空白直角三角形的面积即得阴影部分的面积．
（3）阴影的面积等于两个正方形的面积加上最上面阴影三角形的面积和减去两个空白三角形的面积，列式解答即可．

解答： 解：（1）1×6-（6-2）×1÷2
=6-2
=4（平方米）
答：阴影部分的面积为4平方米．

（2）3×4÷5=2.4（米）
（5+7）×2.4÷2-3×4÷2
=28.8-6
=22.8（平方米）
答：阴影部分的面积为22.8平方米．

（3）8×8+6×6-8×8÷2-（8+6）×6÷2
=64+36-32-42
=26（平方米）
答：阴影部分的面积为26平方米．

点评：此题考查组合图形面积的计算方法，解决此题关键是先弄清楚阴影部分是怎么样得到的，再选用合适的方法解答即可．