
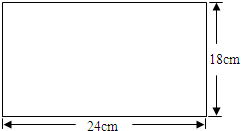
 把一张长24厘米,宽18厘米的长方形的硬纸块(如图)裁成同样大小,面积尽可能大的正方形,纸块没有剩余,至少可以裁多少个这样的正方形?
把一张长24厘米,宽18厘米的长方形的硬纸块(如图)裁成同样大小,面积尽可能大的正方形,纸块没有剩余,至少可以裁多少个这样的正方形? 分析 裁成同样大小,且没有剩余,就是裁成的小正方形的边长是24和18的公因数,要求面积最大的正方形就是以24和18的最大公因数为小正方形的边长,然后用长方形纸片的长和宽分别除以小正方形的边长,就是长方形铁片的长边最少可以裁几个,宽边最少可以裁几个,最后把它们乘起来即可.
解答 解:24=2×2×2×3,
18=3×2×3,
所以24和18的最大公因数是:2×3=6;,即小正方形的边长是6厘米,
长方形纸片的长边可以分;24÷6=4(个),
宽边可以分:18÷6=3(个),
一共可以分成:4×3=12(个);
答:至少可以裁12个这样的正方形.
点评 本题关键是理解:裁成同样大小,且没有剩余,就是裁成的小正方形的边长是24和18的公因数;用到的知识点:两个数的公有质因数连乘积是最大公约数,两个数的公有质因数与每个数独有质因数的连乘积是最小公倍数.


 英才计划期末调研系列答案
英才计划期末调研系列答案科目:小学数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{10}{15}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com