
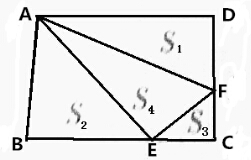
 把长9米、宽6米的长方形分成如图所示的四个三角形,其面积分别是S1,S2,S3,S4,且S1=S2=S3+S4,则S4=15平方米.
把长9米、宽6米的长方形分成如图所示的四个三角形,其面积分别是S1,S2,S3,S4,且S1=S2=S3+S4,则S4=15平方米. 分析 已知长方形的长和宽可以求出长方形的面积,因为S1=S2=S3+S4,所以用长方形的面积除以3即可得到S1、S2的值以及S3+S4的和,再依据三角形的面积公式,可求出图中BE和DF的长,然后用长方形的长和宽分别减去BE和DF,求出EC和FC的长,从而求出S3的值,再用S3+S4的和减去S3即可得到S4的值,据此解答即可.
解答 解:长方形的面积为:9×6=54(平方米);
因为S1=S2=S3+S4,
所以S1=S2=S3+S4=54÷3=18(平方米);
所以BE=18×2÷6=6(米),
DF=18×2÷9=4(米),
所以CE=BC-BE=9-6=3(米),
CF=DC-DF=6-4=2(米),
所以S3=CE×CF÷2
=3×2÷2
=3(平方米),
所以S4=S3+S4-S3
=18-3
=15(平方米);
答:S4=15平方米.
故答案为:15.
点评 本题解决的关键是能灵活的运用三角形的面积公式求出BE和DF的长,从而求出S3所对应三角形的底和高,最后求出其面积.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
 建房子用的“人字梁”主要由三根木头组成.如图.
建房子用的“人字梁”主要由三根木头组成.如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com