
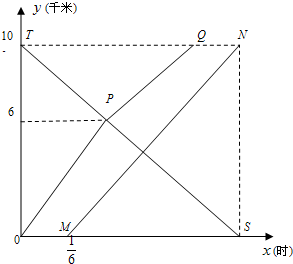
 如图,三人在相距10千米的两地练习骑自行车,折线OPQ、线段MN和TS分别表示甲、乙和丙距某地的路程y与时间x之间的函数关系.已知甲以18千米/时的速度走完6千米后改变速度匀速前进,20分钟到达终点.求乙和丙从甲出发多少分钟相遇,相遇点距甲出发地多少千米?
如图,三人在相距10千米的两地练习骑自行车,折线OPQ、线段MN和TS分别表示甲、乙和丙距某地的路程y与时间x之间的函数关系.已知甲以18千米/时的速度走完6千米后改变速度匀速前进,20分钟到达终点.求乙和丙从甲出发多少分钟相遇,相遇点距甲出发地多少千米? 分析 甲变速,易知折线OPQ表现的是甲的行程.20分=$\frac{1}{3}$小时,甲以18千米/时的速度走完6千米,所以走完6千米用了$\frac{1}{3}$时,设乙和丙从甲出发x分钟相遇,相遇点距甲出发地y千米,已知TS经过T(0,10),P($\frac{1}{3}$,6),设它的表达式y=kx+10,解得k=-12,所以TS表达式y=-12x+10.当y=0时,-12x+10=0,解得x=$\frac{5}{6}$,所以S坐标($\frac{5}{6}$,0)MN经过M($\frac{1}{6}$,0),N($\frac{5}{6}$,10)用同上的方法,求得MN表达式为y=15x-$\frac{15}{6}$,联立y=-12x+10,y=15x-$\frac{15}{6}$,解得x=$\frac{25}{54}$,y=$\frac{40}{9}$.
解答 解:
设乙和丙从甲出发x分钟相遇,相遇点距甲出发地y千米,
已知TS经过T(0,10),P($\frac{1}{3}$,6),
设它的表达式y=kx+10,解得k=-12,
所以TS表达式y=-12x+10.
当y=0时,-12x+10=0,
解得x=$\frac{5}{6}$
所以S坐标($\frac{5}{6}$,0)MN经过M($\frac{1}{6}$,0),N($\frac{5}{6}$,10)
用同上的方法,求得MN表达式为
y=15x-$\frac{15}{6}$
联立y=-12x+10
y=15x-$\frac{15}{6}$
解得:
x=$\frac{25}{54}$
y=$\frac{40}{9}$.
答:乙和丙从甲出发$\frac{25}{54}$分钟相遇,相遇点距甲出发地$\frac{40}{9}$千米.
点评 本题考查了一次函数的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com