练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    图中阴影部分：甲的面积（　　）乙的面积．
    分析：如图，四边形ABCD是一个梯形，三角形ABC与三角形DCB是同底等高的三个三角形，面积相等，两个面积相等的三角形都减去同一个三角形OBC，剩下的两个三角甲、乙的面积相等．
    解答：解：如图，

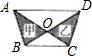
    因为△ABC与△DCB是同底等高的三角形，
    所以△ABC与△DCB的面积相等，
    又因为△ABC的面积-△OBC的面积=甲的面积，△DCB的面积-△OBC的面积=乙的面积，
    所以甲的面积=乙的面积（等量减等量差相等）．
    故选：C．
    点评：关键是根据梯形的特征，两底平行，由于平行线间的距离处处相等，因此三角形ABC与三角形DCB是同底等高的三个三角形，面积相等，再根据等量减等量差相等即可求出甲的面积等于乙的面积．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：

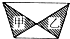    （2011?新泰市）图中阴影部分，甲的面积（　　）乙的面积．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    （2011?市中区）右图中阴影部分占正六边形面积的 
    (     )(     )
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    图中阴影部分是大三角形面积的
    1
    6
    ，是小三角形面积的
    1
    4
    ，大、小两个小三角形面积比为
    3：2
    3：2
    ．

    查看答案和解析>>

    科目：小学数学 来源： 题型：

    精英家教网如图正方形ABCD的边长是8cm，正方形CEFG的边长是6cm．求图中阴影部分三角形BFD的面积．

    查看答案和解析>>

    同步练习册答案