


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:
| A、一个圆柱体,如果它的底面半径扩大到原来的2倍,高不变,那么它的侧面积也扩大到原来的2倍 | ||||
| B、长方形、正方形和圆都是轴对称图形,圆的对称轴最多 | ||||
| C、折线统计图既能清楚地表示数量的多少,又能反映数量的增减变化情况 | ||||
D、已知A、B是两个不等于0的自然数,如果A>B,那么
|
查看答案和解析>>
科目:小学数学 来源: 题型:单选题
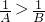
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com