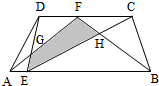
考点:三角形面积与底的正比关系
专题:平面图形的认识与计算
分析:因为D为BC中点,所以三角形ABD和三角形ACD等底等高,所以三角形ABD的面积是24÷2=12平方厘米;同理,E为AD中点,所以三角形BDE、三角形ABE、三角形DEC和三角形ACE的面积都是12÷2=6平方厘米,所以三角形BCE:三角形ACE=(6+6):6=2:1,所以根据燕尾定律可知:AF:FB=1:2,所以三角形BFE的面积是:6÷(1+2)×2=4平方厘米,然后把三角形BDE和三角形BFE的面积相加.
解答:
解:连接BE两点,
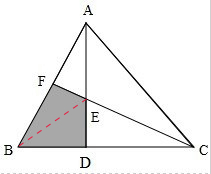
因为D为BC中点,所以三角形ABD和三角形ACD等底等高,所以三角形ABD的面积是24÷2=12平方厘米;
同理,E为AD中点,所以三角形BDE、三角形ABE、三角形DEC和三角形ACE的面积都是12÷2=6平方厘米,
所以,三角形BCE:三角形ACE=(6+6):6=2:1,
所以,根据燕尾定律可知:AF:FB=1:2,所以三角形BFE的面积是:6÷(1+2)×2=4(平方厘米),
所以,三角形BDE和三角形BFE的面积和即阴影部分面积是:4+6=10(平方厘米).
答:阴影部分的面积是10平方厘米.
点评:本题考查了三角形面积与底的正比关系和燕尾定律的综合应用.

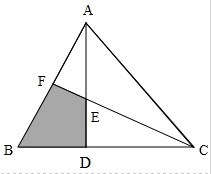 已知△ABC的面积为24cm2,D为BC中点,E为AD中点,求阴影部分面积.
已知△ABC的面积为24cm2,D为BC中点,E为AD中点,求阴影部分面积.