
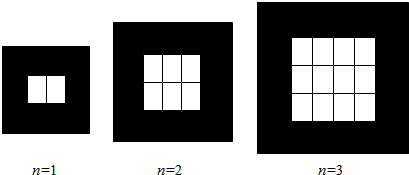
 乐乐和妈妈决定用同样规律的黑白两色的正方形瓷砖铺设地面,请观察瓷砖的图形,回答下列问题:在n=6的图形中有42块白瓷砖,在第n个图中,共有n(n+1)块白瓷砖(用含n的代数式表示)
乐乐和妈妈决定用同样规律的黑白两色的正方形瓷砖铺设地面,请观察瓷砖的图形,回答下列问题:在n=6的图形中有42块白瓷砖,在第n个图中,共有n(n+1)块白瓷砖(用含n的代数式表示) 分析 观察题中三个长方体中白块瓷砖所拼的图形是长方形,分析块数可知,所拼成长方形的长和宽都逐一增加.
解答 解:第1个图中有白块瓷砖的块数为:2×1=2(块);
第2个图中有白块瓷砖的块数为:3×2=(2+1)×2=6(块);
第3个图中有白块瓷砖的块数为:4×3=(3+1)×3=12(块);
…
第n个图中有白块瓷砖的块数为:n(n+1)块.
所以在第6个图中,共有:
6×(6+1)=42(块).
答:在n=6的图形中有42块白瓷砖,在第n个图中,共有n(n+1)块白瓷砖.
故答案为:42,n(n+1).
点评 本题考查了一元二次方程的应用及图形的变化类问题,解决这类问题首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com